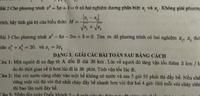p= $\frac{\sqrt{x} }{x-9}$ Tìm x để P đạt giá trị lớn nhất
Hãy luôn nhớ cảm ơn và vote 5*
nếu câu trả lời hữu ích nhé!
TRẢ LỜI
$#CheliKa$
`P = (sqrt{x})/(x+9)` `(` `x ≥ 0` `)`
`P = 1/((x+9)/(sqrt{x}))`
Để `P` lớn nhất thì `(x+9)/sqrt{x}` nhỏ nhất.
Ta có :
`(x+9)/(sqrt{x}) = x/(sqrt{x}) + 9/(sqrt{x}) = sqrt{x} + 9/sqrt{x}`
Áp dụng bất đẳng thức `AM` `-` `GM` :
`sqrt{x} + 9/(sqrt{x}) ≥ 2 sqrt{sqrt{x} . 9/sqrt{x} }`
`→` `sqrt{x} + 9/(sqrt{x}) ≥ 2 sqrt{9}`
`→` `sqrt{x} + 9/(sqrt{x}) ≥ 6`
Dấu " `=` " xảy ra khi `sqrt{x} = 9/sqrt{x} ⇔ x = 9` `(tm)`
Vậy : Tại `x = 9` thì Max `P = 1/6` .
Hãy giúp mọi người biết câu trả lời này thế nào?
Ta có :`x>=0`.
Với `x=0` thì `P=0`. Với `x\ne0`:
Xét biểu thức `Q=(x+9)/(\sqrt(x))=\sqrt(x) + 9/(\sqrt(x))`
Áp dụng bất đẳng thức Cauchy, ta có:
`\sqrt(x) + 9/(\sqrt(x)) >= 2\sqrt(\sqrt(x) . 9/(\sqrt(x)) )=6`.
`=>Q>=6`. Mà `Q=1/P` nên `P<=1/6`.
Vậy GTLN của P là `1/6`, đạt được khi `\sqrt(x) = 9/(\sqrt(x)) <=>x=9`.
Hãy giúp mọi người biết câu trả lời này thế nào?
Bạn muốn hỏi điều gì?
Bảng tin
Bạn muốn hỏi điều gì?
 Inbox: m.me/hoidap247online
Inbox: m.me/hoidap247online Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.
Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.