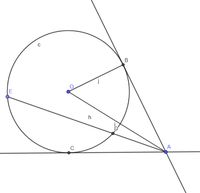
mng ơi giải giúp mik mai mik ktra rồi Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O), các đường cao BD và CE cắt nhau tại H. Gọi F và K lần lượt là giao điểm của AH với BC, DE a) Chứng minh: Tứ giác ADHE nội tiếp đường tròn và xác định tâm I của đường tròn. b) Chứng minh: DB là phân giác của góc EDF và $\frac{KH}{HF}$ =$\frac{DK}{DF}$

a) - Do BD và CE là hai đường cao của ΔABC nên BD ⊥ AC và CE ⊥ AB

  ⇒ ∧ADB = 90* và ∧AEC=90*

    - Tứ giác ADHE có ∧ADH + ∧AEH = 90* + 90* = 180*

  ⇒ Tứ giác ADHE nội tiếp đường tròn

    - Gọi I là trung điểm của AH

   ΔADH vuông tại D có I là trung điểm của AH nên IA = ID = IH

   ΔAEH vuông tại E có I là trung điểm của AH nên IA = IE = IH

  ⇒ IA = ID = IH = IE

  Do đó I là tâm của đường tròn ngoại tiếp tứ giác ADHE

b) - ΔABC có 2 đường cao BD và CE

  Mà BD ∩ CE tại H nên H là trực tâm ΔABC ⇒ AH ⊥ BC hay HF ⊥ BC 

  ⇒ ∧HFC = 90*

   - tứ giác HDCF có: ∧HDC + ∧HFC = 90* + 90* = 180*

  ⇒ tứ giác HDCF nội tiếp đường tròn

  ⇒ ∧HDF = ∧HCF và ∧DCF = ∧AHD

  Tứ giác ADHE nội tiếp đường tròn có: ∧AHD = ∧AED

  ⇒ ∧AED = ∧DCB

  Tứ giác EDCB nội tiếp đường tròn ⇒ ∧EDB = ∧ECB

  Mà ∧EBC = ∧HDF (cmt)

  ⇒ ∧EDB = ∧HDF hay ∧KDH = ∧HDF

  ⇒ DB là phân giác của góc EDF

    - ΔDKF có DB là tia phân giác ⇒ KH/HF = DK/DF