

Hãy luôn nhớ cảm ơn và vote 5*
nếu câu trả lời hữu ích nhé!
TRẢ LỜI
Dưới đây là ý tưởng của me dựa theo sách đã làm:
Phân tích:
Gọi 3 cạnh của `triangleABC ` là `a,b,c`
Theo công thức diện tích:
`S_(ABC)=(a.h_a)/2=(b.h_b)/2=(c.h_c)/2`
`=>ah_a=bh_b=ch_c`
`=>a/h_b=b/h_a=c/[(h_a h_b)/h_c]`
`=>a,b,c` tỉ lệ với `h_a;h_b;(h_a.h_b)/h_c`
Biết `h_a;h_b;h_c ` ta dựng `k=(h_a.h_b)/h_c`
Do đó ta được một tam giác đồng dạng với tam giác phải dựng
Cách dựng: Dựng `triangleAB'C'` có `AB'=k,AC'=h_a;B'C'=h_b`
Dựng đường cao `AH'`
Trên `AH' ` đặt `AH=h_a`
Qua `H ` dựng đường thẳng song song với `B'C'` , cắt `AB';AC' ` ở `B,C` ta được `triangleABC`
Chứng minh:
Gọi `BD;CE` là các đường cao của `triangleABC`
Ta đi chứng minh `BD=h_b;CE=h_c`
Tỉ số 2 đường cao bằng tỉ số nghịch đảo của 2 cạnh tương ứng nên:
`(AH)/(BD)=(AC)/(BC)`
`=>(h_a)/(BD)=(AC)/(BC)`
Lại có `(AC)/(BC)=(AC')/(B'C')=(h_a)/(h_b)`
DO đó `(h_a)/(BD)=(h_a)/(h_b)`
`=>BD=h_b`
Chứng minh tương tự `=>CE=h_c`
Biện luận:
Bài toán có 1 nghiệm hình `<=>` dựng được `triangleAB'C'`
`<=>|h_a-h_b|<(h_a.h_b)/(h_c)<h_a+h_b`
`<=>|1/(h_b)-1/(h_a)|<1/(h_c)<1/(h_a)+1/(h_b)`
Hãy giúp mọi người biết câu trả lời này thế nào?
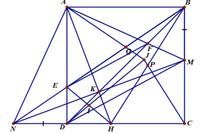
Đáp án:
Giải thích các bước giải:
Dựng tam giác ABC có 3 đườn cao cho trc là ha hb hc
Hãy giúp mọi người biết câu trả lời này thế nào?
Bạn ơi phải phân tích với nêu cách vẽ chứ
oke
vào nhóm mình không ạ
B1: Vẽ hình tam giác B2: Từ Điểm A - Đặt một cạnh góc vuông của ê-ke trùng với đường thẳng BC - Trượt ê-ke theo đường thẳng để cạnh góc vuông còn lại của ê-ke gặp điểm A, vạch đường cao AH theo cạnh đó B3: Điểm B tương tự nhe b4: điểm c tương tự nhe
Bạn muốn hỏi điều gì?
Bảng tin
Bạn muốn hỏi điều gì?
 Inbox: m.me/hoidap247online
Inbox: m.me/hoidap247online Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.
Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.












