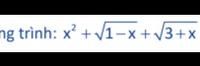Giai phuong trinh........
Hãy luôn nhớ cảm ơn và vote 5*
nếu câu trả lời hữu ích nhé!
TRẢ LỜI
`x^2 + \sqrt{1-x} + \sqrt{3 + x} = 2x + 1`
ĐKXĐ: `-1/2 ≤ x ≤ 1`
`⇔ \sqrt{1-x} + \sqrt{3 + x} = -x^2 + 2x + 1`
`⇔ \sqrt{1-x} + \sqrt{3 + x} = -(x^2 - 2x + 1) + 2`
$⇔ \sqrt{1-x} + \sqrt{3 + x} = 2 - (x - 1)^2\ (*)$
Áp dụng BĐT `\sqrt{a} + \sqrt{b} ≥ \sqrt{a + b}\ (` dấu $``$$="$ xảy ra khi: `ab=0)`, ta có:
`\sqrt{1-x} + \sqrt{3 + x} ≥ \sqrt{1-x+3+x}= 2`
Mà: `2 - (x - 1)^2 ≤ 2`
`⇒` Để PT $(*)$ xảy ra thì:
$\begin{cases} (1-x)(3+x) = 0\\(x - 1)^2 = 0\\ \end{cases}$
`⇔ x = 1\ \text{(TM)}`
Vậy nghiệm của PT là: `S = {1}`
Hãy giúp mọi người biết câu trả lời này thế nào?
`x^2+\sqrt(1-x)+\sqrt(3+x)=2x+1(-1/2<=x<=1)`
`<=>\sqrt(1-x)+\sqrt(3+x)=-(x-1)^2+2`
Áp dụng bđt `\sqrta+\sqrtb>=\sqrt(a+b)` cho `VT` ta được:
`\sqrt(1-x)+\sqrt(3+x)>=\sqrt(1-x+3+x)=\sqrt4=2(1)`
Ta có: `VP=-(x-1)^2+2<=2` `(do` `-(x-1)^2<=0)(2)`
`=>VT=VP=2`
Dấu "`=`" xảy ra `(1)<=>(1-x)(3+x)=0`
`<=>[(x=1(TM)),(x=-3(KTM)):}`
Dấu "`=`" xảy ra `(2)<=>-(x-1)^2=0`
`<=>x=1(TM)`
Vậy `S={1}` là tập nghiệm của pt.
Hãy giúp mọi người biết câu trả lời này thế nào?
Bạn muốn hỏi điều gì?
Bảng tin
Bạn muốn hỏi điều gì?
 Inbox: m.me/hoidap247online
Inbox: m.me/hoidap247online Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.
Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.