Đăng nhập để hỏi chi tiết
tìm tập xác định của hàm số sau (căn 2+sinx)-(1/(tan^2x-1))
Hãy luôn nhớ cảm ơn và vote 5*
nếu câu trả lời hữu ích nhé!
TRẢ LỜI
- quangcuong347
- Câu trả lời hay nhất!
Đây là một chuyên gia không còn hoạt động
Bạn xem hình
Hãy giúp mọi người biết câu trả lời này thế nào?
52 vote
`~rai~`
\(\sqrt{2+\sin x}-\dfrac{1}{tan^2x-1}\\ĐKXĐ:\begin{cases}2+\sin x\ge 0\\\cos x\ne 0\\\tan^2x\ne 1.\end{cases}\quad(1)\\\text{Ta có:}-1\le \sin x\le 1\quad\forall x\\\Leftrightarrow 1\le 2+\sin x\le 3\quad\forall x\\\Rightarrow 2+\sin x>0\quad\forall x\quad nên \\(1)\Leftrightarrow \begin{cases}\cos x\ne 0\\\tan^2x\ne 1\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\dfrac{\sin^2x}{\cos^2x}\ne 1\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\sin^2x\ne \cos^2x\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\cos^2x-\sin^2x\ne 0\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\cos2x\ne 0\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\2x\ne\dfrac{\pi}{2}+k\pi\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{\pi}{4}+k\dfrac{\pi}{2}.\end{cases}\quad(k\in\mathbb{Z})\\D=\mathbb{R}\backslash\left\{\dfrac{\pi}{2}+k\pi;\dfrac{\pi}{4}+k\dfrac{\pi}{2}\Big|k\in\mathbb{Z}\right\}.\)
Hãy giúp mọi người biết câu trả lời này thế nào?
51 vote
Lệnh latex dài dữ \sqrt{2+\sin x}-\dfrac{1}{tan^2x-1}\\ĐKXĐ:\begin{cases}2+\sin x\ge 0\\\cos x\ne 0\\\tan^2x\ne 1.\end{cases}\quad(1)\\\text{Ta có:}-1\le \sin x\le 1\quad\forall x\\\Leftrightarrow 1\le 2+\sin x\le 3\quad\forall x\\\Rightarrow 2+\sin x>0\quad\forall x\quad nên \\(1)\Leftrightarrow \begin{cases}\cos x\ne 0\\\tan^2x\ne 1\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\dfrac{\sin^2x}{\cos^2x}\ne 1\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\sin^2x\ne \cos^2x\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\cos^2x-\sin^2x\ne 0\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\cos2x\ne 0\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\2x\ne\dfrac{\pi}{2}+k\pi\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{\pi}{4}+k\dfrac{\pi}{2}.\end{cases}\quad(k\in\mathbb{Z})\\D=\mathbb{R}\backslash\left\{\dfrac{\pi}{2}+k\pi;\dfrac{\pi}{4}+k\dfrac{\pi}{2}\Big|k\in\mathbb{Z}\right\}. Rút gọnLệnh latex dài dữ \sqrt{2+\sin x}-\dfrac{1}{tan^2x-1}\\ĐKXĐ:\begin{cases}2+\sin x\ge 0\\\cos x\ne 0\\\tan^2x\ne 1.\end{cases}\quad(1)\\\text{Ta có:}-1\le \sin x\le 1\quad\forall x\\\Leftrightarrow 1\le 2+\sin x\le 3\quad\forall x\\\Rightarrow 2+\sin x>... xem thêm
\sqrt{2+\sin x}-\dfrac{1}{tan^2x-1}\\ĐKXĐ:\begin{cases}2+\sin x\ge 0\\\cos x\ne 0\\\tan^2x\ne 1.\end{cases}\quad(1)\\\text{Ta có:}-1\le \sin x\le 1\quad\forall x\\\Leftrightarrow 1\le 2+\sin x\le 3\quad\forall x\\\Rightarrow 2+\sin x>0\quad\forall x\quad nên \\(1)\Leftrightarrow \begin{cases}\cos x\ne 0\\\tan^2x\ne 1\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\dfrac{\sin^2x}{\cos^2x}\ne 1\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\sin^2x\ne \cos^2x\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\cos^2x-\sin^2x\ne 0\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\\cos2x\ne 0\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\2x\ne\dfrac{\pi}{2}+k\pi\end{cases}\\\Leftrightarrow \begin{cases}x\ne\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{\pi}{4}+k\dfrac{\pi}{2}.\end{cases}\quad(k\in\mathbb{Z})\\D=\mathbb{R}\backslash\left\{\dfrac{\pi}{2}+k\pi;\dfrac{\pi}{4}+k\dfrac{\pi}{2}\Big|k\in\mathbb{Z}\right\}. Rút gọn\sqrt{2+\sin x}-\dfrac{1}{tan^2x-1}\\ĐKXĐ:\begin{cases}2+\sin x\ge 0\\\cos x\ne 0\\\tan^2x\ne 1.\end{cases}\quad(1)\\\text{Ta có:}-1\le \sin x\le 1\quad\forall x\\\Leftrightarrow 1\le 2+\sin x\le 3\quad\forall x\\\Rightarrow 2+\sin x>0\quad\forall x\qu... xem thêm
Bạn muốn hỏi điều gì?
Đặt câu hỏiTham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Bảng tin
Bạn muốn hỏi điều gì?
Đặt câu hỏi
Cơ quan chủ quản: Công ty Cổ phần Công nghệ Giáo dục Thành Phát
Tải ứng dụng
Inbox: m.me/hoidap247online
Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.
Giấy phép thiết lập mạng xã hội trên mạng số 331/GP-BTTTT do Bộ Thông tin và Truyền thông.
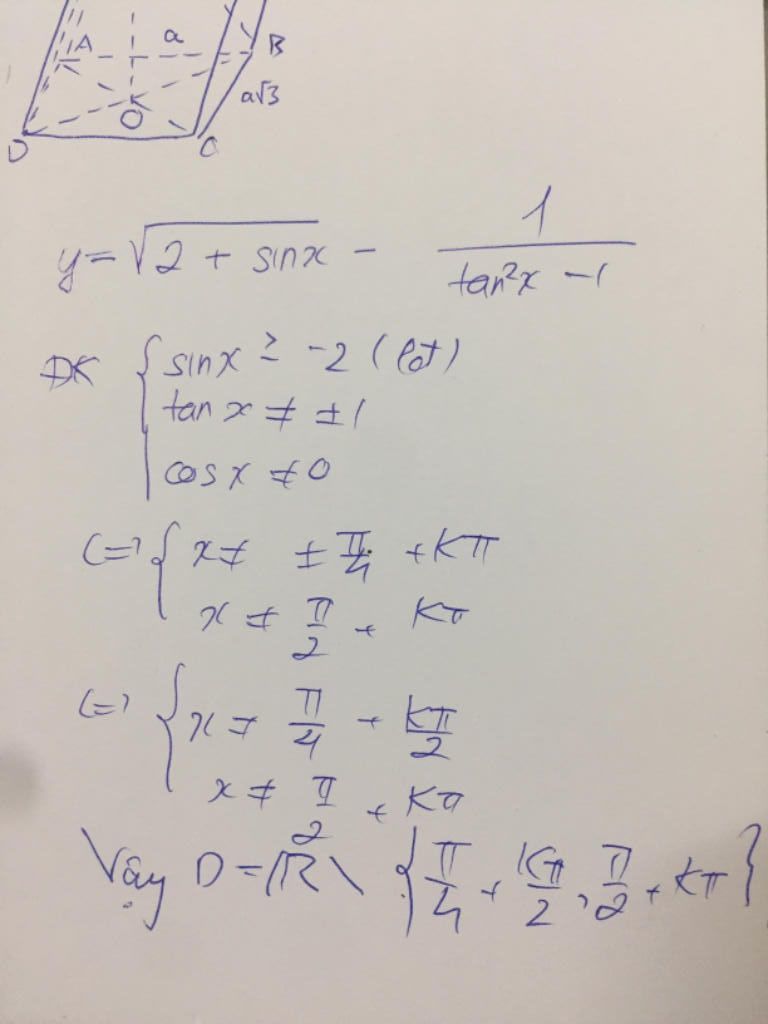
130
3840
142
https://hoidap247.com/thong-tin-ca-nhan/838632 bạn này spam nhiều anh ạ