

Các bạn ơi help mi pờ lít
Hãy luôn nhớ cảm ơn và vote 5*
nếu câu trả lời hữu ích nhé!
TRẢ LỜI
Dựng tam giác cân $ABC$ có $\widehat{A} = 36^o$ với độ dài cạnh $BC = 1$
$\Rightarrow \widehat{B} = \widehat{C} = 72^o$
Từ $C$ kẻ đường phân giác $CD \, (D\in AB)$
$\Rightarrow \widehat{ACD} = \widehat{BAC} = 36^o$
$\Rightarrow AD = DC$
Ta lại có: $\widehat{B} = \widehat{BDC} = 72^o$
$\Rightarrow DC = BC$
Do đó $AD = DC = BC = 1$
Từ $D$ kẻ đường cao $DH$ ứng với cạnh $AC \, (H\in AC)$
$\Rightarrow AH = HC$
Đặt $AH = HC = x \, (x > 0)$
Ta được:
$cos\widehat{A} = \dfrac{AH}{AD} = x$
$\Rightarrow BD = AB - AD = AC - AD = 2x - 1$
Áp dụng tính chất đường phân giác, ta được:
$\dfrac{AD}{BD} = \dfrac{AC}{BC}$
$\Leftrightarrow \dfrac{1}{2x - 1} = \dfrac{2x}{1}$
$\Leftrightarrow 4x^2 - 2x - 1 = 0$
$\Leftrightarrow \left[\begin{array}{l}x = \dfrac{1 + \sqrt{5}}{4}\\x = \dfrac{1 - \sqrt{5}}{4} < 0 \,\, \, (loại)\end{array}\right.$
Vậy $cos36^o = \dfrac{1 + \sqrt{5}}{4}$
Hãy giúp mọi người biết câu trả lời này thế nào?
Bạn muốn hỏi điều gì?
Bảng tin
Bạn muốn hỏi điều gì?
 Inbox: m.me/hoidap247online
Inbox: m.me/hoidap247online Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.
Trụ sở: Tầng 7, Tòa Intracom, số 82 Dịch Vọng Hậu, Cầu Giấy, Hà Nội.

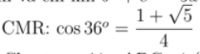








0
10
0
hinh oi ban oi hinh dau r